공정 능력 분석에 대한 통계 상세 정보
이 섹션에는 레거시 관리도에서 공정 능력 분석 보고서의 통계량 계산에 대한 상세 정보가 포함되어 있습니다.
변동 통계량
모든 공정 능력 분석에서 사용하는 계산식은 동일합니다. 옵션은 다음과 같이 시그마(s) 계산 방식에 차이가 있습니다.
장기 시그마
전체 표준편차를 사용합니다. 이 옵션은 Ppk 통계량에 사용되며 다음과 같이 시그마를 계산합니다.
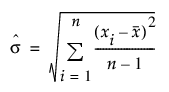
참고: 기본적으로 장기 시그마 보고서의 공정 능력 지수는 다른 시그마 보고서에 사용되는 Cp 라벨을 사용합니다. 장기 시그마 보고서에 Ppk 라벨을 사용하려면 파일 > 환경 설정 > 플랫폼 > 분포 > PpK 공정 능력 라벨 환경 설정을 선택하십시오.
관리도 시그마
관리도 설정에 따라 결정된 시그마를 사용합니다.
– 관리도 시작 창의 "통계량 지정" 버튼을 사용하여 "시그마" 값을 지정하면 지정된 값이 공정 능력 지수 계산에 사용됩니다.
– "이동 범위(평균)" 옵션을 사용하는 IR 차트에서는 시그마 값이 다음과 같이 계산됩니다.
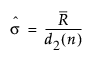
다음은 각 요소에 대한 설명입니다.
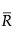= 이동 범위의 평균
d2(n) = 단위 표준편차를 갖는 n개 독립 정규 분포 변수의 범위 기대값. 여기서 n은 "범위 길이" 옵션의 값입니다.
– "이동 범위 중앙값" 옵션을 사용하는 IR 차트에서는 시그마 값이 다음과 같이 계산됩니다.
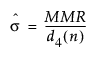
다음은 각 요소에 대한 설명입니다.
MMR = 비결측 이동 범위의 중앙값
d4(n) = 단위 표준편차를 갖는 n개 독립 정규 분포 변수의 범위 중앙값. 여기서 n은 "범위 길이" 옵션의 값입니다.
– "R" 옵션을 사용하는 Xbar 차트에서는 시그마 값이 다음과 같이 계산됩니다.
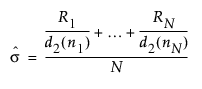
다음은 각 요소에 대한 설명입니다.
Ri = i번째 부분군의 범위
ni = i번째 부분군의 표본 크기
d2(ni) = 단위 표준편차를 갖는 ni개 독립 정규 분포 변수의 범위 기대값
N = 부분군 수(ni ≥ 2)
– "S" 옵션을 사용하는 Xbar 차트에서는 시그마 값이 다음과 같이 계산됩니다.
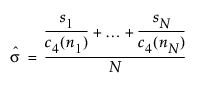
다음은 각 요소에 대한 설명입니다.
ni = i번째 부분군의 표본 크기
c4(ni) = 단위 표준편차를 갖는 ni개 독립 정규 분포 변수의 표준편차 기대값
N = 부분군 수(ni ≥ 2)
si = i번째 부분군의 표본 표준편차
정규 분포에 대한 공정 능력 지수
이 섹션에서는 정규 데이터에 대한 공정 능력 지수의 계산에 대해 자세히 설명합니다.
평균이 m이고 표준편차가 s인 공정 특성에 대한 모집단 기반 공정 능력 지수는 다음과 같이 정의됩니다.
Cp =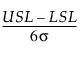 
Cpl =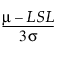 
Cpu =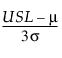 
Cpk =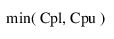 
Cpm =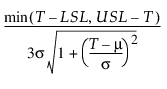 
다음은 각 요소에 대한 설명입니다.
LSL = 규격 하한
USL = 규격 상한
T = 목표값
표본 기반 공정 능력 지수의 경우 모수는 추정값으로 대체됩니다. s의 추정값은 공정 능력 분석 창에서 지정한 방법을 사용합니다. 자세한 내용은 변동 통계량에서 확인하십시오.
규격 한계가 하나뿐인 경우 결측 규격 한계를 포함하는 공정 능력 지수가 결측값으로 보고됩니다.
팁: 공정 능력 지수 1.33은 허용 가능한 최소값으로 간주되는 경우가 많습니다. 정규 분포의 경우 공정 능력 지수 1.33은 100,000개당 약 6개의 기대 부적합 단위 수에 해당합니다.
공정 능력 지수에 대한 신뢰 구간
참고: 공정 능력 지수에 대한 신뢰 구간은 장기 시그마 보고서에만 나타납니다.
Cp에 대한 100(1 - a)% 신뢰 구간은 다음과 같이 계산됩니다.
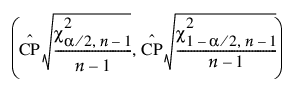
다음은 각 요소에 대한 설명입니다.
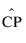= Cp에 대한 추정값
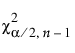= 자유도가 n - 1인 카이제곱 분포의 (a/2)번째 분위수
n = 관측값 수
Cpk에 대한 100(1 - a)% 신뢰 구간은 다음과 같이 계산됩니다.
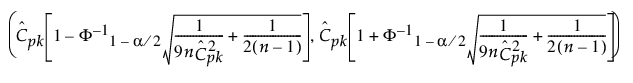
다음은 각 요소에 대한 설명입니다.
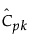= Cpk에 대한 추정값
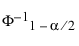= 표준 정규 분포의 (1 - a/2)번째 분위수
n = 관측값 수
CPM에 대한 100(1 - a)% 신뢰 구간은 다음과 같이 계산됩니다.
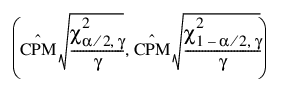
다음은 각 요소에 대한 설명입니다.
= CPM에 대한 추정값
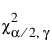= 자유도가 g인 카이제곱 분포의 (a/2)번째 분위수
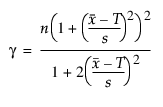
n = 관측값 수
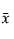= 관측값의 평균
T = 목표값
s = 장기 시그마 추정값
참고: CPM에 대한 신뢰 구간은 목표값이 규격 하한과 규격 상한 사이에서 중심화되는 경우에만 계산됩니다.
CPL과 CPU의 신뢰 하한 및 상한은 Chou et al. (1990)의 방법을 사용하여 계산됩니다.
CPL에 대한 100(1 - a)% 신뢰 한계(CPLL, CPLU로 표시)는 다음 방정식을 충족합니다.
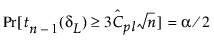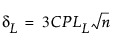
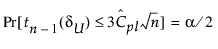여기서, 
여기서,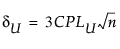 
다음은 각 요소에 대한 설명입니다.
tn-1(d)은 n - 1 자유도와 비중심성 모수 d를 사용하는 비중심 t 분포를 따릅니다.
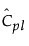= Cpl에 대한 추정값
CPU에 대한 100(1 - a)% 신뢰 한계(CPUL, CPUU로 표시)는 다음 방정식을 충족합니다.
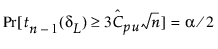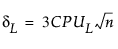
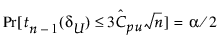여기서, 
여기서,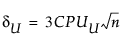 
다음은 각 요소에 대한 설명입니다.
tn-1(d)은 n - 1 자유도와 비중심성 모수 d를 사용하는 비중심 t 분포를 따릅니다.
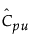= Cpu에 대한 추정값
비정규 분포에 대한 공정 능력 지수
이 섹션에서는 비정규 분포에 대한 공정 능력 지수를 계산하는 방법을 설명합니다. 이러한 일반화된 공정 능력 지수는 다음과 같이 정의됩니다.
Cp =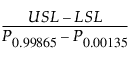 
Cpk =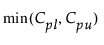 
Cpm =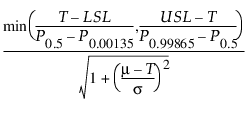 
Cpl =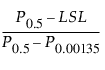 
Cpu =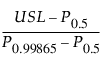 
다음은 각 요소에 대한 설명입니다.
LSL = 규격 하한
USL = 규격 상한
T = 목표값
Pα = 적합 분포의 a*100번째 백분위수
Cpm 계산에서 m와 s는 적합 분포의 기대값 및 분산 제곱근을 사용하여 추정됩니다. 모수 추정값 보고서의 모수와 적합 분포의 기대값 및 분산 간의 관계에 대한 자세한 내용은 기본 분석의 연속형 적합 분포에 대한 통계 상세 정보 및 이산형 적합 분포에 대한 통계 상세 정보에서 확인하십시오.
시그마 품질 통계량
각 부분(LSL 아래, USL 위, 규격 밖 전체)에 대한 시그마 품질 통계량은 다음과 같이 계산됩니다.
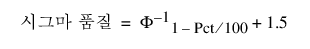
다음은 각 요소에 대한 설명입니다.
Pct = 보고서에서 "백분율" 열의 값
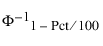= 표준 정규 분포의 (1 - Pct/100)번째 분위수
참고: LSL 아래 백분율과 USL 위 백분율을 합하면 규격 밖 전체 백분율 값이 되지만 LSL 아래 시그마 품질과 USL 위 시그마 품질을 합하면 규격 밖 전체 시그마 품질 값이 되지는 않습니다. 시그마 품질을 계산할 때는 정규 분포 분위수 찾기가 포함되어 가산되지 않기 때문입니다.
벤치마크 Z 통계량
벤치마크 Z 통계량은 정규 분포를 기반으로 하는 공정 능력 분석에만 사용할 수 있습니다. 벤치마크 Z 통계량은 다음과 같이 계산됩니다.
Z Bench =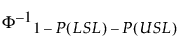 
Z LSL =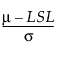 
= 3 * Cpl
Z USL =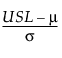 
= 3 * Cpu
다음은 각 요소에 대한 설명입니다.
LSL = 규격 하한
USL = 규격 상한
m = 표본 평균
s = 표본 표준편차
F-11 - P(LSL) - P(USL) = 표준 정규 분포의 (1 - P(LSL) -P(USL))번째 분위수
P(LSL) = Prob(X < LSL) = 1 - F(Z LSL).
P(USL) = Prob(X > USL) = 1 - F(Z USL).
F = 표준 정규 누적 분포 함수