이산형 적합 분포에 대한 통계 상세 정보
이 섹션에는 분포 플랫폼의 "이산형 적합" 메뉴 옵션에 대한 통계 상세 정보가 포함되어 있습니다. 별도로 지정한 경우를 제외하고 모수 추정값에 대한 신뢰 구간은 가능도 기반 계산을 사용합니다. 가능도 기반 신뢰 구간에 대한 자세한 내용은 예측 및 전문 모델링의 프로파일 가능도 신뢰 한계에 대한 통계 상세 정보에서 확인하십시오.
Poisson 적합
Poisson 분포는 단일 척도 모수 l > 0을 갖습니다.
pmf: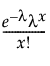 
(단, 0 £ l < ¥, x = 0,1,2,...)
E(x) = l
Var(x) = l
Poisson 분포는 이산형 분포이므로 해당 중첩 곡선은 각 정수에서 도약이 나타나는 계단 함수입니다.
음이항 적합
음이항 분포는 지정된 실패 횟수에 도달하기 전의 성공 횟수를 모델링하는 데 유용합니다. 다음 파라미터화 계산식에는 평균 모수 l와 산포 모수 s가 포함되어 있습니다.
pmf: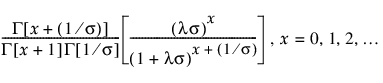 
E(x) = l
Var(x) = l + sl2
여기서 G(·)는 Gamma 함수입니다.
음이항 분포와 감마 Poisson 분포 간의 관계
음이항 분포는 감마 Poisson 분포와 동등합니다. 감마 Poisson 분포는 데이터가 몇 가지 Poisson(m) 분포의 조합이고 각 Poisson(m) 분포의 m이 다른 경우에 유용합니다.
감마 Poisson 분포는 x|m가 Poisson 분포를 따르고 m가 Gamma(a,t) 분포를 따른다고 가정한 결과입니다. 감마 Poisson에는 l = at 및 s = t+1 모수가 있습니다. s 모수는 산포 모수입니다. s > 1이면 과대산포가 나타납니다. 즉, x에서 Poisson만으로 설명할 경우보다 더 많은 변동이 나타납니다. s = 1이면 x가 Poisson(l)으로 축소됩니다.
pmf: 
(단, 0 < l, 1 ≤ s, x = 0,1,2,...)
E(x) = l
Var(x) = ls
여기서 G(·)는 Gamma 함수입니다.
감마 Poisson 분포는 snegbin = (sgp - 1) / lgp인 음이항 분포와 동등합니다.
모수 l 및 s를 갖는 감마 Poisson 분포를 모수 l를 갖는 Poisson 분포와 비교하려면 JMP Samples/Scripts 폴더에 있는 demoGammaPoisson.jsl을 실행하십시오.
ZI Poisson 적합
ZI(영과잉) Poisson 분포는 척도 모수 l > 0과 영과잉 모수 p를 갖습니다.
pmf: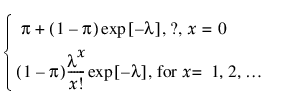 
E(x) = (1 - p)l
Var(x) = l(1 - p)(1 + lp)
ZI 음이항 적합
ZI(영과잉) 음이항 분포는 척도 모수 l > 0, 산포 모수 s > 0 및 영과잉 모수 p를 갖습니다.
pmf: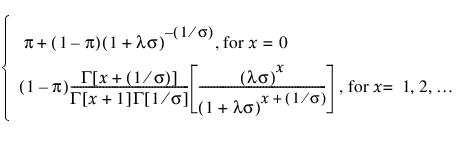 
E(x) = (1 - p)l
Var(x) = l(1 - p)[1 + l(s + p)]
이항 적합
"이항 적합" 옵션은 두 가지 형식의 데이터(상수 표본 크기 또는 표본 크기가 포함된 열)를 허용합니다.
pmf: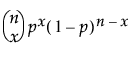 
(단, 0 £ p £ 1, x = 0,1,2,...,n)
E(x) = np
Var(x) = np(1-p)
여기서 n은 독립 시행 횟수입니다.
참고: 이항 분포 모수의 신뢰 구간은 프로파일 가능도 구간입니다.
베타 이항 적합
베타 이항 분포는 데이터가 몇 가지 Binomial(p) 분포의 조합이고 각 Binomial(p) 분포의 p가 다른 경우에 유용합니다. 한 예로, 제조 라인 간에 평균 결함 수(p)가 다른 경우 여러 라인에서 결합된 전체 결함 수를 들 수 있습니다.
베타 이항 분포는 x|p가 Binomial(n,p) 분포를 따르고 p가 Beta(a,b)를 따른다고 가정한 결과입니다. 베타 이항 분포는 모수 p = a/(a+b) 및 d = 1/(a+b+1)를 갖습니다. 모수 d는 산포 모수입니다. d > 1이면 과대산포가 나타납니다. 즉, x에서 이항 분포만으로 설명할 경우보다 더 많은 변동이 나타납니다. d < 0이면 과소산포가 나타납니다. d = 0이면 x가 Binomial(n,p) 분포를 따릅니다. 베타 이항 분포는 n ³ 2일 때만 존재합니다.
pmf: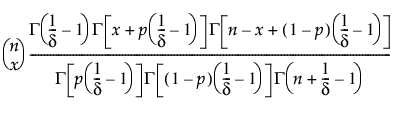 
(단,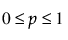 
, 
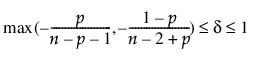, x = 0,1,2,...,n)
E(x) = np
Var(x) = np(1-p)[1+(n-1)d]
여기서 G(·)는 Gamma 함수입니다.
x|p ~ Binomial(n,p)인 반면 p ~ Beta(a,b)임을 기억하십시오. 모수 p = a/(a+b) 및 d = 1/(a+b+1)는 플랫폼에 의해 추정됩니다. a 및 b의 추정값을 구하려면 다음 계산식을 사용합니다.
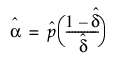
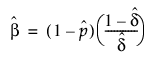
d의 추정값이 0인 경우에는 이 계산식이 적용되지 않습니다. 이 경우에는 베타 이항 분포가 Binomial(n,p)로 축소된 것이며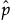 
는 p의 추정값입니다.
베타 이항 분포 모수의 신뢰 구간은 프로파일 가능도 구간입니다.
산포 모수 d를 갖는 베타 이항 분포를 모수 p 및 n = 20을 갖는 이항 분포와 비교하려면 JMP Samples/Scripts 폴더에 있는 demoBetaBinomial.jsl을 실행하십시오.
ZI 이항 적합
"ZI 이항 적합" 옵션은 두 가지 형식의 데이터(상수 표본 크기 또는 표본 크기가 포함된 열)를 허용합니다.
pmf: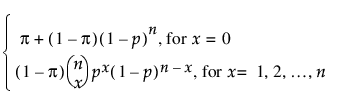 
E(x) = (1-p)np
Var(x) = (1-p)[np(1-p) + n2p2] - [(1-p)np]2
여기서 n은 독립 시행 횟수입니다.
ZI 베타 이항 적합
"ZI 베타 이항 적합" 옵션은 두 가지 형식의 데이터(상수 표본 크기 또는 표본 크기가 포함된 열)를 허용합니다. ZI 베타 이항 분포는 n ³ 2일 때만 존재합니다.
pmf: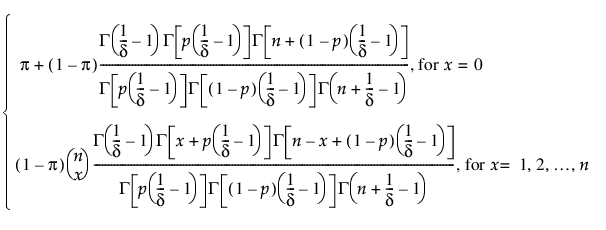 
E(x) = (1-p)np
Var(x) = (1-p)np[(1-p)(1 + (n-1)d) + np] - [(1-p)np]2
여기서 n은 독립 시행 횟수입니다.