연속형 적합 분포에 대한 통계 상세 정보
이 섹션에는 분포 플랫폼의 "연속형 적합" 메뉴 옵션에 대한 통계 상세 정보가 포함되어 있습니다. 별도로 지정한 경우를 제외하고 모수 추정값에 대한 신뢰 구간은 가능도 기반 계산을 사용합니다. 가능도 기반 신뢰 구간에 대한 자세한 내용은 예측 및 전문 모델링의 프로파일 가능도 신뢰 한계에 대한 통계 상세 정보에서 확인하십시오. Y 열에 "감지 한계" 열 특성이 있는 경우 "연속형 적합" 옵션은 중도절단 분포를 적합시키고 분포의 일부만 사용할 수 있습니다. 중도절단 데이터에 분포를 적합시키는 방법에 대한 자세한 내용은 Meeker and Escobar(1998) 연구 자료에서 확인하십시오.
정규 적합
"정규 적합" 옵션은 정규 분포의 두 모수를 추정합니다.
• m(평균) - x 축에서의 분포 위치를 정의합니다.
• s(표준편차) - 분포의 산포 또는 퍼짐 정도를 정의합니다.
표준 정규 분포는 m = 0이고 s = 1일 때 나타납니다.
pdf: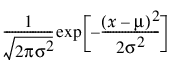 
(단, 
, 
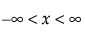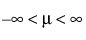, 0 < s)
E(x) = m
Var(x) = s2
참고: 평균 추정값에 대한 신뢰 구간은 t 분포를 기반으로 합니다. 척도 모수에 대한 신뢰 구간은 c2 분포를 기반으로 합니다.
Cauchy 적합
"Cauchy 적합" 옵션은 위치가 m이고 척도가 s인 Cauchy 분포를 적합시킵니다.
pdf: 
(단,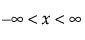 
, 
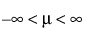, 0 < s)
E(x) = 정의되지 않음
Var(x) = 정의되지 않음
스튜던트 t 적합
"스튜던트 t 적합" 옵션은 위치가 m이고, 척도가 s이고, 자유도가 n인 스튜던트 t 분포를 적합시킵니다.
pdf: 
(단,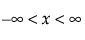 
, 
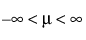, 0 < s, 1 ≤ n)
E(x) = m (단, 1 < n)
Var(x) = s2n/(n-2) (단, 2 < n)
참고: n = 1인 경우 스튜던트 t 분포는 Cauchy 분포와 동일합니다.
SHASH 적합
"SHASH 적합" 옵션은 SHASH(SinH-ArcSinH) 분포를 적합시킵니다. SHASH 분포는 정규 분포의 변환을 기반으로 하며 정규 분포를 특수한 경우로 포함합니다. 이 분포는 대칭적일 수도 있고 비대칭적일 수도 있습니다. 형태는 두 개의 형상 모수 g 및 d에 의해 결정됩니다. SHASH 분포에 대한 자세한 내용은 Jones and Pewsey 연구 자료(2009)에서 확인하십시오.
pdf: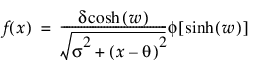 
(단, 
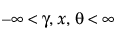, 0 < d, s)
다음은 각 요소에 대한 설명입니다.
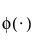- 표준 정규 pdf입니다.
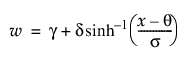
• g = 0이고 d = 1인 경우 SHASH 분포는 위치가 q이고 척도가 s인 정규 분포와 동등합니다.
• 변환 sinh(w)는 m = 0이고 s = 1인 정규 분포를 따릅니다.
ZI SHASH 적합
"ZI SHASH 적합" 옵션은 ZI(영과잉) SHASH(SinH-ArcSinH) 분포를 적합시킵니다. 영과잉 SHASH 분포는 점질량이 0인 SHASH 분포와 동일합니다. 이 분포는 대칭적일 수도 있고 비대칭적일 수도 있습니다.
pdf: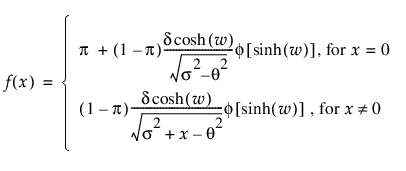 
(단, 
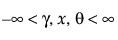; 0 < d, s)
다음은 각 요소에 대한 설명입니다.
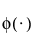- 표준 정규 pdf입니다.
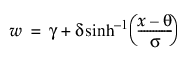
참고: ZI SHASH 분포 모수 추정값에 대한 신뢰 구간은 Wald 기반 계산을 사용합니다.
지수 적합
지수 분포는 생존 데이터와 같이 시간 경과에 따라 무작위로 발생하는 사건을 설명하는 데 특히 유용합니다. 지수 분포는 중복되지 않는 사건의 발생 사이 경과 시간을 모델링하는 데도 유용할 수 있습니다. 중복되지 않는 사건의 예로는 사용자의 컴퓨터 쿼리 후 서버에서 응답할 때까지의 시간, 서비스 데스크에서의 고객 내방, 전화 교환대에서의 전화 수신 등이 포함됩니다.
지수 분포는 b = 1이고 a = s일 경우 특수한 형태의 2모수 Weibull 분포가 되며, a = 1일 경우에는 특수한 형태의 감마 분포가 되기도 합니다.
pdf: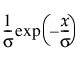 
(단, 0 < s, 0 ≤ x)
E(x) = s
Var(x) = s2
Devore 연구 자료(1995)에 따르면 지수 분포는 무기억성을 가집니다. 무기억성은 t시간 후 여전히 유효한 어떤 성분을 확인할 경우 추가 수명의 분포(t시간 후까지도 해당 성분이 유지된 경우 추가 수명의 조건부 확률)가 원래 분포와 동일함을 의미합니다.
ExGaussian 적합
"ExGaussian 적합" 옵션은 정규 분포와 지수 분포를 합한 분포를 적합시킵니다. ExGaussian 옵션은 정규 분포 부분의 위치(m) 및 척도(s) 모수와 지수 분포 모수(l)를 추정합니다.
pdf: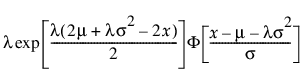 
(단, 
; 
; 0 < s, l)
여기서 F(·)는 표준 정규 cdf입니다.
E(x) = m + 1/l
Var(x) = s2 + 1/l2
지수 수정 가우시안 분포에 대한 자세한 내용은 Ament et al. (2019) 및 Palmer et al. (2011)에서 확인하십시오. 일부 소스의 경우 지수 분포 부분의 파라미터화가 다릅니다. "ExGaussian 적합" 옵션의 파라미터화는 분포 플랫폼의 "지수 적합" 옵션에 사용되는 파라미터화의 역수를 사용합니다.
감마 적합
"감마 적합" 옵션은 감마 분포 모수 a > 0 및 s > 0을 추정합니다. 적합 감마 보고서에서 모수 a(알파)는 형태 또는 곡률을 설명합니다. 모수 s(시그마)는 분포의 척도 모수입니다. 데이터는 0보다 커야 합니다.
pdf: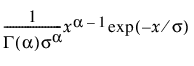 
(단, 0 < x; 0 < a, s)
E(x) = as
Var(x) = as2
• 표준 감마 분포의 경우 s = 1입니다. 시그마는 값이 1이 아닐 경우 가로 축을 따라 분포를 늘리거나 줄이므로 척도 모수라고 합니다.
• 카이제곱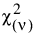 
분포는 s = 2이고 a = n/2일 때 발생합니다.
• 지수 분포는 a = 1일 때 발생합니다.
표준 감마 밀도 함수는 a ≤ 1일 때는 감소하기만 합니다. a > 1일 때 밀도 함수는 0에서 시작하여 최대값까지 증가하다가 감소합니다.
로그 정규 적합
"로그 정규 적합" 옵션은 2모수 로그 정규 분포의 m(척도) 및 s(형상) 모수를 추정합니다. X = ln(Y)가 정규 분포인 경우에만 Y 변수가 로그 정규 분포로 나타납니다. 데이터는 0보다 커야 합니다.
pdf: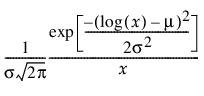 
(단,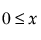 
, 
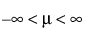, 0 < s)
E(x) =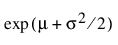 
Var(x) =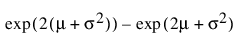 
Weibull 적합
Weibull 분포는 a(척도) 및 b(형태) 값에 따라 다른 형태로 나타납니다. 이 함수는 특히 기계 장치 및 생물학 분야에서 수명 길이를 추정하는 데 적절한 모형을 제공하는 경우가 많습니다.
Weibull 분포의 pdf는 다음과 같이 정의됩니다.
pdf: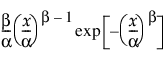 
(단, a,b > 0, q < x)
E(x) =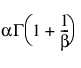 
Var(x) = 
여기서 G(·)는 Gamma 함수입니다.
정규 2 혼합 적합 및 정규 3 혼합 적합
"정규 2 혼합 적합" 및 "정규 3 혼합 적합" 옵션은 두 개 또는 세 개의 정규 분포를 혼합하여 적합시킵니다. 이러한 유연한 분포는 이봉 또는 다봉 데이터를 적합시킬 수 있습니다. 각 그룹에 대해 평균, 표준편차 및 전체 대비 비율이 개별적으로 추정됩니다. 다음 방정식에서 k는 혼합되는 정규 분포의 수와 같습니다.
pdf: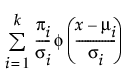 
E(x) =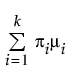
Var(x) =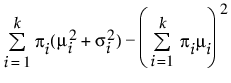
여기서 mi, si 및 pi는 각각 i번째 그룹의 평균, 표준편차 및 비율이며 f(·)는 표준 정규 pdf입니다.
참고: 정규 혼합 분포 모수 추정값에 대한 신뢰 구간은 Wald 기반 계산을 사용합니다.
Johnson 적합
"Johnson 적합" 옵션은 Johnson 분포 체계에서 최적의 적합 분포를 선택하여 적합시키며, Johnson 분포 체계에 포함된 세 개의 분포는 모두 하나의 변환된 정규 분포를 기반으로 합니다. 이 세 가지 분포는 다음과 같습니다.
• Johnson Su - 경계가 없습니다.
• Johnson Sb - 양쪽 꼬리에 경계가 있습니다. 이 경계는 추정 가능한 모수에 의해 정의됩니다.
• Johnson Sl - 한쪽 꼬리에 경계가 있습니다. 이 경계는 추정 가능한 모수에 의해 정의됩니다. Johnson Sl 계열에는 로그 정규 분포 계열이 포함됩니다.
선택된 분포에 대한 적합만 보고됩니다. Johnson 분포의 선택 프로시저 및 모수 추정에 대한 자세한 내용은 Slifker and Shapiro 연구 자료(1980)에서 확인할 수 있습니다. 모수 추정에는 최대 가능도가 사용되지 않습니다.
Johnson 분포는 유연하기 때문에 널리 사용됩니다. 특히 Johnson 분포 체계는 왜도와 첨도의 가능한 모든 조합을 지원하므로 데이터 적합 기능 면에서 주목됩니다. 하지만 SHASH 분포 또한 매우 유연하므로 Johnson 분포보다 권장됩니다.
Z가 표준 정규 변량인 경우 이 분포 체계는 다음과 같이 정의됩니다.
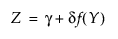
다음은 Johnson Su의 경우에 해당하는 각 요소에 대한 설명입니다.
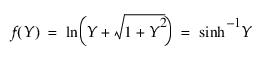
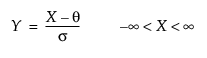
다음은 Johnson Sb의 경우에 해당하는 각 요소에 대한 설명입니다.
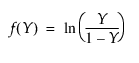
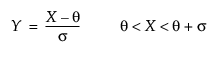
다음은 Johnson Sl의 경우(단, s = ±1)에 해당하는 각 요소에 대한 설명입니다.
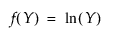
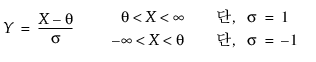
Johnson Su
pdf: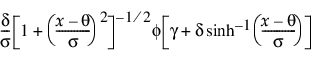 
(단, -¥ < x, q, g < ¥, 0 < q,d)
Johnson Sb
pdf: 
(단, q < x < q+s, 0 < s)
Johnson Sl
pdf: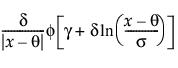 
(단, s = 1일 경우 q < x, s = -1일 경우 q > x)
여기서 f(·)는 표준 정규 pdf입니다.
참고: Johnson 분포 모수 추정값에 대한 신뢰 구간은 Wald 기반 계산을 사용합니다.
베타 적합
베타 분포는 간격 0,1 사이에 들어가도록 제한된 확률 변수의 동작을 모델링하는 데 유용합니다. 예를 들어 비율은 항상 0에서 1 사이입니다. "베타 적합" 옵션은 두 개의 형상 모수, 즉 a > 0 및 b > 0을 추정합니다. 베타 분포에서는 값이 0,1 구간에만 있습니다.
pdf: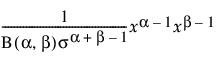 
(단, 0 < x < 1, 0 < s,a,b)
E(x) =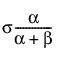 
Var(x) =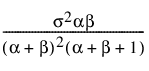 
여기서 B(·)는 베타 함수입니다.
전체 적합
"분포 비교" 보고서에서는 분포 목록이 AICc를 기준으로 오름차순 정렬됩니다. 체크박스를 사용하여 선택한 분포에 대한 적합 보고서를 표시하거나 숨기고 분포 곡선을 중첩 표시할 수 있습니다.
AICc와 BIC의 계산식은 다음과 같이 정의됩니다.
AICc =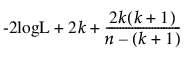 
BIC =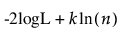 
다음은 각 요소에 대한 설명입니다.
– logL은 로그 가능도입니다.
– n은 표본 크기입니다.
– k는 모수 수입니다.
"AICc 가중치" 열은 합계가 1이 되는 정규화된 AICc 값을 보여 줍니다. AICc 가중치는 적합된 분포 중 하나가 true일 때 특정 분포가 true 분포일 확률로 해석됩니다. 따라서 AICc 가중치가 1과 가장 가까운 분포가 더 적절한 적합입니다. AICc 가중치는 비결측 AICc 값만 사용해서 계산됩니다.
AICcWeight = exp[-0.5(AICc-min(AICc))] / sum(exp[-0.5(AICc-min(AICc))])
여기서 min(AICc)는 적합된 분포 중에서 가장 작은 AICc 값입니다.
"분포 비교" 보고서의 측도에 대한 자세한 내용은 선형 모형 적합의 가능도, AICc 및 BIC에서 확인하십시오.