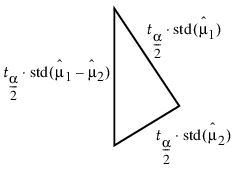비교 원에 대한 통계 상세 정보
일원 분석 플랫폼에서 비교 원은 다중 비교 검정의 LSD(최소 유의차)를 그래픽으로 표현한 것입니다. 이 최소 유의차는 확률 분위수에 두 평균의 차이에 대한 표준 오차를 곱한 값입니다. "개별 쌍 비교" 옵션의 경우 Fisher LSD가 사용되며 확률 분위수는 스튜던트 t 통계량입니다. 이 경우에 대한 비교 원 계산을 보여 줍니다. LSD는 다음과 같이 정의됩니다.
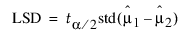
두 독립 평균의 차이에 대한 표준 오차는 다음 관계식으로 계산됩니다.
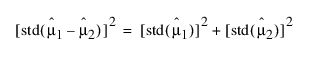
평균 간에 상관관계가 없는 경우 이러한 통계량은 다음과 같은 관계를 갖습니다.
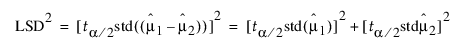
이러한 제곱 값 간에는 Figure 6.41에 그래픽으로 표시된 직각 삼각형의 경우처럼 피타고라스 관계식이 성립됩니다.
그림 6.41 두 평균 간의 차이 관계
이 삼각형의 빗변은 평균을 비교하기 위한 척도가 됩니다. 실제 차이가 빗변(LSD)보다 큰 경우에만 평균이 유의하게 다른 것으로 간주됩니다.
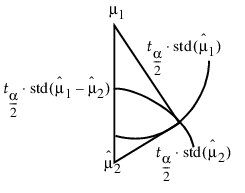
두 평균이 정확히 경계선에 있고 실제 차이는 최소 유의차와 동일하다고 가정해 보겠습니다. 세로 척도에서 측정된 평균 값을 꼭지점으로 하는 삼각형을 그려 봅니다. 또한 각 평균을 중심으로 하고 해당 평균의 신뢰 구간을 지름으로 하는 원을 그려 봅니다.
그림 6.42 t-검정 통계량의 기하학적 관계
각 원의 반지름은 삼각형의 해당 변 길이, 즉 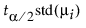 입니다.
입니다.
원은 삼각형의 변과 동일하게 직각으로 교차해야 하며 그 관계는 다음과 같습니다.
• 평균이 정확히 최소 유의차만큼 다르면 각 평균을 중심으로 한 신뢰 구간 원이 직각으로 교차합니다. 즉, 탄젠트 각도가 직각입니다.
이제 평균 간에 최소 유의차보다 크거나 작은 차이가 있을 때 원이 교차하는 방식을 살펴보겠습니다.
• 원의 교차 외각이 직각보다 큰 경우에는 평균이 유의하게 다르지 않은 것입니다. 원의 교차 외각이 직각보다 작은 경우에는 평균이 유의하게 다른 것입니다. 즉, 외각이 90도 미만이면 평균이 최소 유의차에서 멀리 떨어져 있는 것입니다.
• 원이 교차하지 않으면 평균이 유의하게 다른 것입니다. 원이 내포 관계에 있으면 평균이 유의하게 다르지 않은 것입니다(Figure 6.9).
스튜던트 t 대신 다른 확률 분위수 값을 사용하여 다양한 다중 비교 검정에 이와 동일한 그래픽 기법을 적용할 수 있습니다.