공간 및 시간 변동성에 대한 통계 상세 정보
단순 모형 yi = m + ei를 가정해 보겠습니다. 모형 적합 플랫폼의 혼합 모형 분석법에서 공간 또는 시간 구조는 오차 항 ei를 통해 모델링됩니다. 일반적으로 공간 상관 모형은 Var(ei) = si2 및 Cov(ei, ej) = sij로 정의할 수 있습니다.
si가 yi의 위치를 나타낸다고 하겠습니다. 이때 si는 공간 또는 시간을 반영하는 좌표로 지정됩니다. 일반적으로 공간 또는 시간 구조는 공분산이 si와 sj 사이의 유클리드 거리 dij에 대한 함수라고 가정하여 제한됩니다. 공분산은 Cov(ei, ej) = s2[f(dij)]로 작성할 수 있으며, 여기서 f(dij)는 관측값 yi와 yj 간의 상관을 나타냅니다.
둘 이상의 위치 좌표가 있는 경우 f(dij)가 방향에 종속되지 않으면 공분산 구조가 등방성입니다. 그렇지 않으면 구조가 이방성입니다.
공간 상관 구조
JMP에서 사용할 수 있는 공간 모형의 상관 구조는 아래와 같습니다. 이러한 구조는 제약된 경우 외에는 양수인 r에 의해 파라미터화됩니다.
• 구형
여기서,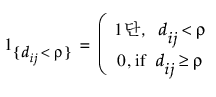 
• 지수
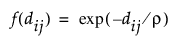
• 가우시안
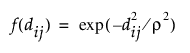
• 거듭제곱
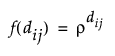
이방성 모형의 경우 상관 함수는 각 방향에 대해 rκ 모수를 포함합니다.
변동도
공간 과정이 2차 정상 상태인 경우 공간 상관 구조에 나열된 구조는 변동도를 정의합니다. 지리 통계학에서 차용된 변동도는 공간 변동을 설명하고 추정하는 표준 도구입니다. 여기에서는 반분산을 사용하여 관측값 간의 거리 dij에 대한 함수로 공간 변동을 측정합니다.
Z(s)가 위치 s에서 반응의 값을 나타낸다고 하겠습니다. si와 sj에서 관측값 간의 반분산은 다음과 같이 정의됩니다.
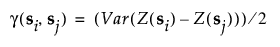
반응에 상수 평균이 있으면 표현식을 다음과 같이 단순화할 수 있습니다.
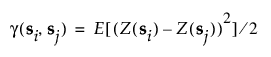
등방성 과정의 경우 반분산은 점 사이의 거리(h)에만 종속되며 함수를 다음과 같이 지정할 수 있습니다.
다음은 변동도와 관련된 용어입니다.
너겟
절편으로 정의됩니다. 너겟은 h = 0에서 불연속 이동을 나타냅니다.
문턱(Sill)
더 먼 거리에 대해 도달한 평탄 시작 구간에서의 반변동도 값으로 정의됩니다. 이 값은 관측값의 분산에 해당합니다. 너겟 효과가 없는 모형에서 문턱(sill)은 s2입니다. 너겟 효과가 있는 모형에서 문턱(sill)은 s2 + c1이며, 여기서 c1은 너겟을 나타냅니다. 부분 문턱(sill)은 s2으로 정의됩니다.
범위
반변동도가 문턱(sill)에 도달하는 거리로 정의됩니다. 범위 미만의 거리에서는 관측값이 공간적으로 상관됩니다. 범위를 초과하거나 같은 거리의 경우 공간 상관은 사실상 0입니다. 구형 모형에서 r는 범위입니다. 지수 모형에서는 3r가 실제적 범위입니다. 가우시안 모형에서는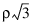 
이 실제적 범위입니다. 실제적 범위는 공분산이 문턱(sill)의 95%로 축소되는 거리로 정의됩니다.
Figure 8.34에서 반복 효과 공분산 모수 추정값은 다양한 반변동도 특징을 나타냅니다.
공간 구형
범위(r)의 추정값입니다.
너겟
c1의 척도화된 추정값입니다. 잔차 x 너겟이 c1입니다.
잔차
너겟이 없는 모형의 문턱(sill) 또는 부분 문턱(sill)입니다.
변동도 추정값
지정된 등방성 공간 구조에 대해 추정된 변동도는 공간 상관 구조에 나오는 적절한 함수에 대한 관측 데이터의 비선형 최소 제곱 적합을 사용하여 구할 수 있습니다.
경험적 반분산
경험적 반분산을 계산하려면 변동도 공분산을 위해 선택된 변수에 대한 모든 점 쌍 사이의 거리가 계산됩니다. 거리 범위는 10개의 동일 구간으로 구분됩니다. 데이터에 10개의 구간이 허용되지 않으면 가능한 한 많은 구간이 생성됩니다.
점 쌍으로 구성된 거리 클래스가 생성됩니다. h번째 거리 클래스는 거리가 h번째 구간에 속하는 모든 점 쌍으로 구성됩니다.
다음 표기를 고려하십시오.
n
점 쌍의 총 수
Ch
거리가 h번째로 큰 구간에 속하는 점으로 구성된 거리 클래스
Z(x)
x에서 반응의 값(x = 시간 또는 공간 좌표의 벡터)
g(h)
거리 클래스 Ch에 대한 반분산
반분산 함수(g)는 다음과 같이 정의됩니다.
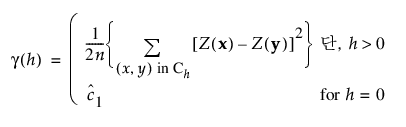
여기서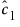 
은 너겟 효과의 추정값입니다.