특이값 분해
SVD(특이값 분해)를 사용하면 선형 변환을 회전, 척도화, 다른 회전으로 표현할 수 있습니다. SVD에 따르면 n x p 행렬 X를 다음과 같이 쓸 수 있습니다.
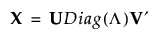
r을 X의 계수라고 하겠습니다. r x r 단위 행렬을 Ir로 나타냅니다.
U, Diag(L) 및 V 행렬은 다음과 같은 특성을 가집니다.
U는 U¢U = Ir인 n x r 반직교 행렬입니다.
V는 V¢V = Ir인 p x r 반직교 행렬입니다.
Diag(L)는 열 벡터 L = (l1, l2, ..., lr)¢로 지정되는 양수 대각 요소가 포함된 r x r 대각 행렬입니다. 여기서 l1 ³ l2 ³ ... ³ lr > 0입니다.
li는 X의 0이 아닌 특이값입니다.
다음은 SVD를 정방 행렬의 스펙트럼 분해와 관련시킵니다.
• li의 제곱은 X¢X의 0이 아닌 고유값입니다.
• V의 r 열은 X¢X의 고유 벡터입니다.
참고: 문헌에는 U, V 행렬 및 특이값을 포함하는 행렬의 차원과 관련된 다양한 규칙이 있습니다. 그러나 차이가 X의 계수까지의 분해에 실제적인 영향을 미치지 않습니다.
특이값 분해에 대한 자세한 내용은 Press et al. (1998, Section 2.6) 연구 자료에서 확인하십시오.
공분산 행렬
이 섹션에서는 SVD(특이값 분해)를 사용하여 공분산 행렬의 고유 벡터와 고유값을 구하는 방법을 설명합니다. 관심 행렬이 적어도 하나의 큰 차원을 갖는 경우 SVD를 계산하는 것이 공분산 행렬 및 고유값 분해를 계산하는 것보다 훨씬 더 효율적입니다.
n을 관측값 수, p를 관심 있는 다변량 분석에 포함된 변수의 수라고 하겠습니다. 데이터 값의 n x p 행렬을 X로 나타냅니다.
SVD는 대개 표준화된 데이터에 적용됩니다. 값을 표준화하려면 평균을 뺀 후 표준편차로 나눕니다. 표준화된 데이터 값의 n x p 행렬을 Xs로 나타냅니다. 그러면 표준화된 데이터의 공분산 행렬은 X의 상관 행렬이며 다음과 같이 정의됩니다.
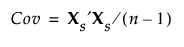
SVD를 Xs에 적용하여 Xs¢Xs의 고유 벡터와 고유값을 얻을 수 있습니다. 이렇게 하면 X 행렬이 심한 가로형(열이 많음) 또는 세로형(행이 많음)일 때 고유 벡터와 고유값을 효율적으로 계산할 수 있습니다. 이 기법은 와이드 PCA의 기본입니다. 자세한 내용은 주성분 보고서에서 확인하십시오.
공분산 역행렬
일부 다변량 기법을 사용할 때 공분산 행렬의 역행렬을 계산해야 합니다. 이 섹션에서는 SVD를 사용하여 공분산 행렬의 역행렬을 계산하는 방법을 설명합니다.
표준화된 데이터 행렬을 Xs로 나타내고 S = Xs¢Xs를 정의합니다. 특이값 분해를 사용하면 S를 다음과 같이 쓸 수 있습니다.
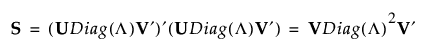
S가 완전 계수이면 V는 p x p 직교정규 행렬이고 S-1을 다음과 같이 쓸 수 있습니다.

S가 완전 계수가 아니면 Diag(L)-1을 일반화 역행렬 Diag(L)+로 대체할 수 있습니다. 여기서 Diag(L)의 대각 요소는 역수로 대체됩니다. 즉, S의 일반화 역행렬이 다음과 같이 정의됩니다.
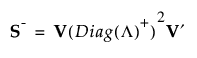
이 일반화 역행렬은 SVD만 사용하여 계산할 수 있습니다.
와이드 선형 판별 분석에 SVD를 적용하는 데 대한 자세한 내용은 와이드 선형 판별 방법에서 확인하십시오.
특이값 분해 계산
다변량 방법 플랫폼에서 JMP는 Golub와 Kahan(1965) 연구 자료에 제안된 방법에 따라 행렬의 SVD를 계산합니다. Golub와 Kahan 방법은 2단계 절차를 포함합니다. 첫 번째 단계에서는 M 행렬을 이중 대각 행렬 J로 축소합니다. 두 번째 단계에서는 J의 특이값을 계산합니다. 이 값은 원래 행렬 M의 특이값과 동일합니다. 일반적으로 M 행렬의 열은 변수가 계산에 미치는 효과를 균등화하기 위해 표준화됩니다. Golub와 Kahan 방법은 계산이 효율적입니다.