 모형 요약
모형 요약
"일반화 회귀" 보고서의 "모형 요약" 섹션에서는 적합된 모형을 설명하고 적합 자체에 대한 요약 정보를 제공합니다.
 모형 설명 상세 정보
모형 설명 상세 정보
"모형 요약" 보고서의 첫 번째 부분에서는 적합된 모형을 설명하는 정보를 제공합니다.
반응
"모형 적합" 창에서 "Y" 역할에 할당된 열입니다. 두 개의 열을 사용하여 구간 중도절단을 지정한 경우 두 열 이름이 모두 나열됩니다.
분포
"모형 적합" 창에서 선택한 분포입니다. 분위수 회귀의 경우 반응에 대해 지정된 분위수 값도 표시됩니다.
추정 방법
"모형 시작" 패널에서 선택한 추정 방법입니다.
검증 방법
"모형 시작" 패널에서 선택한 검증 방법입니다.
평균 모형 연결
"모형 적합" 창에서 선택한 분포를 기반으로 평균에 대한 모형 연결 함수입니다.
위치 모형 연결
위치 모수에 대한 모형 연결 함수이며 "모형 적합" 창에서 "Cauchy" 또는 "t(5)" 분포를 선택한 경우 표시됩니다.
척도 모형 연결
"모형 적합" 창에서 선택한 분포를 기반으로 척도 모수에 대한 모형 연결 함수입니다.
확률 모형 연결
"모형 적합" 창에서 선택한 분포를 기반으로 확률에 대한 모형 연결 함수입니다.
산포 모형 연결
"모형 적합" 창에서 선택한 분포를 기반으로 산포 모수에 대한 모형 연결 함수입니다.
영과잉 모형 연결
"모형 적합" 창에서 선택한 분포를 기반으로 영과잉 모수에 대한 모형 연결 함수입니다.
감지 하한
반응 열에 할당된 "감지 한계" 열 특성에 지정한 감지 하한입니다.
감지 상한
반응 열에 할당된 "감지 한계" 열 특성에 지정한 감지 상한입니다.
중도절단 열
"모형 적합" 창에서 "중도절단" 역할에 할당된 열입니다.
중도절단 코드
오른쪽 중도절단된 관측값을 지정하는 중도절단 열의 값입니다. 이 값은 "모형 적합" 창의 "중도절단 코드" 목록에 지정된 값입니다.
 모형 적합 상세 정보
모형 적합 상세 정보
"모형 요약" 보고서의 두 번째 부분에서는 모형 적합과 관련된 통계량을 제공합니다. "검증 방법"에서 "홀드백" 또는 "검증 열"을 선택하는 경우 이러한 통계량은 훈련 데이터 집합과 검증 데이터 집합에 대해 별도로 계산됩니다. "검증 방법"에서 "K 폴드" 또는 "Leave-One-Out"을 선택하면 "모형 요약" 보고서의 이 부분을 사용할 수 없습니다.
행 수
행 수입니다.
빈도 합
"모형 적합" 창에서 "빈도" 또는 "가중치" 역할에 할당된 열 값의 합입니다.
참고: -1*로그 가능도, BIC, AICc 및 ERIC의 경우 값이 작을수록 좋습니다. 자세한 내용은 가능도, AICc 및 BIC에서 확인하십시오.
-1*로그 가능도
현재 모형에 대한 가능도 함수의 음의 자연 로그입니다. 자세한 내용은 가능도, AICc 및 BIC에서 확인하십시오.
참고: 분위수 회귀에는 -1*로그 가능도를 사용할 수 없습니다.
목적 함수
(분위수 회귀에만 사용 가능) 지정된 분위수 회귀 모형을 적합시키기 위해 최소화되는 함수의 값입니다. 최소화되는 함수는 점검-손실 함수입니다.
모수 수
현재 모형에서 0이 아닌 모수의 수입니다.
BIC
다음과 같이 정의되는 베이지안 정보 기준입니다.
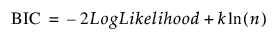
자세한 내용은 가능도, AICc 및 BIC에서 확인하십시오.
AICc
다음과 같이 정의되는 수정 Akaike 정보 기준입니다.
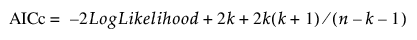
자세한 내용은 가능도, AICc 및 BIC에서 확인하십시오.
ERIC
(지수 계열 분포와 Lasso 회귀 또는 적응형 Lasso 회귀 추정 방법이 지정된 경우에만 사용 가능) 확장된 정규화 정보 기준입니다. 자세한 내용은 Hui et al. 연구 자료 (2015)에서 확인하십시오. ERIC는 다음과 같이 정의됩니다.
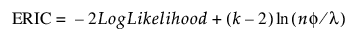
여기서 l는 조정 모수의 값이고 f는 장애 모수입니다.
일반화 R²
(분위수 회귀에는 사용 불가능) 일반 회귀 모형에 적용할 수 있는 R² 측도의 확장입니다. 일반화 R²은 적합 모형의 가능도(LM)를 절편만 있는(상수) 모형의 가능도(L0)와 비교합니다. 이 값은 최대값이 1이 되도록 척도화됩니다. 이항 분포를 제외한 다른 분포의 일반화 R²은 다음과 같이 정의됩니다.
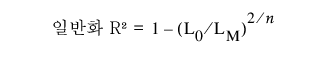
이항 분포가 지정된 경우 일반화 R²은 다음과 같이 정의됩니다.
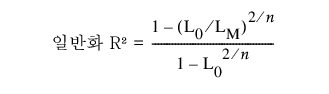
일반화 R² 값이 1이면 완벽한 모형을 나타내고 0이면 상수 모형과 같음을 나타냅니다. 일반화 R² 측도는 표준 최소 제곱 설정 시 연속형 정규 반응에 대한 기존 R²로 단순화됩니다. 일반화 R²을 Nagelkerke 또는 Craig와 Uhler R2이라고도 하는데, 이는 Cox-Snell 유사 R2을 정규화한 것입니다. 자세한 내용은 Nagelkerke 연구 자료(1991)에서 확인하십시오.
참고: 정규 분포가 지정되면 일반화 R²이 R²으로 바뀝니다.
주의: 서로 다른 반응 분포를 사용하는 모형에 대해 일반화 R² 값을 비교하면 안 됩니다. 비교는 주어진 반응 분포를 사용하고 절편만 있는 모형을 대상으로 합니다.
R²
(정규 분포가 지정된 경우에만 사용 가능) 랜덤 오차가 아니라 모형에 기인할 수 있는 반응의 변동 비율을 추정합니다. R² 값이 1이면 완벽한 모형을 나타내고 0이면 상수 모형과 같음을 나타냅니다. R² 값은 다음과 같이 계산됩니다.
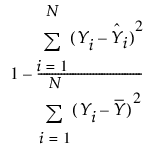
Adj-R²
(정규 분포가 지정되고 추정 방법에 벌점이 포함되지 않은 경우에만 사용 가능) 모형의 모수 수에 대한 R² 통계량을 조정합니다. Adj-R²을 사용하면 모수 수가 다른 모형을 쉽게 비교할 수 있습니다. 계산에 자유도가 사용됩니다. Adj-R² 값은 다음과 같이 계산됩니다.
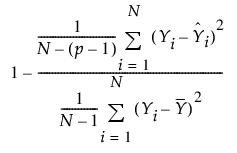
여기서 N은 관측값 수이고 p는 모수 수입니다.
참고: 검증 데이터 집합이 있는 경우 수정 R² 통계량은 훈련 데이터 집합에 대해서만 보고됩니다.
RASE
(정규 분포가 지정된 경우에만 사용 가능) RASE(제곱근 평균 제곱 오차)는 현재 모형에서 평균 제곱 예측 오차의 제곱근입니다. 자세한 내용은 RASE에서 확인하십시오.
람다 벌점
(Dantzig 선택기, Lasso 회귀, Elastic Net, 능형 회귀 및 이중 Lasso 회귀 추정 방법에만 사용 가능) 현재 모형에 대한 조정 모수 l의 값입니다. 자세한 내용은 추정 방법에 대한 통계 상세 정보에서 확인하십시오.