비모수 검정 보고서
일원 분석 플랫폼에는 평균을 비교하는 비모수 옵션이 있습니다. 이 섹션에서는 이러한 방법에 대한 보고서를 다룹니다.
방법에는 그룹 간에 동일한 평균 또는 중앙값 가설에 대한 검정이 포함됩니다. 비모수 검정에는 순위 스코어라고 하는 반응 순위의 함수가 사용됩니다. 자세한 내용은 Hajek(1969) 및 SAS Institute Inc. (2023a)에서 확인하십시오. "비모수 다중 비교" 절차는 쌍별 비교의 전체 오차율을 제어하는 데도 사용할 수 있습니다. 자세한 내용은 비모수 다중 비교 보고서에서 확인하십시오.
Wilcoxon Kruskal-Wallis, 중앙값, Friedman 순위 및 Van der Waerden 검정 보고서
일원 분석 플랫폼의 Wilcoxon Kruskal-Wallis, 중앙값, Friedman 순위 또는 Van der Waerden 검정은 두 개 또는 세 개의 테이블에 요약 통계량과 검정 결과가 제공됩니다. 요약 통계량 테이블에는 다음 열이 포함되어 있습니다.
수준
X의 수준입니다.
개수
각 수준의 빈도입니다.
스코어 합
각 수준의 순위 스코어 합입니다.
기대 스코어
클래스 수준 간에 차이가 없다는 귀무가설하의 기대 스코어입니다.
스코어 평균
각 수준의 평균 순위 스코어입니다.
(평균-평균0)/표준0
표준화된 스코어입니다. 평균0은 귀무가설하의 기대 평균 스코어입니다. 표준0은 귀무가설하의 기대 스코어 합에 대한 표준편차입니다. 귀무가설은 그룹 간에 그룹 평균 또는 중앙값이 동일하다는 것입니다.
2표본 검정, 정규 근사 테이블
X 변수의 수준이 정확히 두 개인 경우 "2표본 검정, 정규 근사" 테이블에 다음 열이 포함됩니다.
S
관측값 수가 더 적은 수준에 대한 순위 스코어의 합입니다.
Z
0.5 연속성 수정을 사용하는 정규 근사 검정에 대한 검정 통계량입니다. 자세한 내용은 2표본 정규 근사에서 확인하십시오.
Prob>Z
0.5 연속성 수정을 사용하는 정규 근사 검정에 대한 단측 p 값입니다. 이 p 값은 표준 정규 분포를 기반으로 합니다.
Prob>|Z|
0.5 연속성 수정을 사용하는 정규 근사 검정에 대한 p 값입니다. 이 p 값은 표준 정규 분포를 기반으로 합니다.
참고: "Wilcoxon/Kruskal-Wallis 검정(순위 합)" 보고서에서는 이 테이블을 "Wilcoxon 2표본 검정, 정규 근사" 테이블이라고 합니다.
일원 검정, 카이제곱 근사 테이블
"일원 검정"(또는 Kruskal-Wallis 검정) 테이블에는 위치에 대한 카이제곱 검정 결과가 포함됩니다. 자세한 내용은 Conover 연구 자료(1999)에서 확인하십시오. 그룹 수가 두 개인 경우 Kruskal-Wallis 검정은 Wilcoxon 검정과 동일합니다.
카이제곱
카이제곱 검정 통계량의 값입니다. 자세한 내용은 일원 카이제곱 근사에서 확인하십시오.
DF
검정의 자유도입니다.
Prob>ChiSq
검정의 p 값입니다. p 값은 자유도가 X의 수준 수에서 1을 뺀 값에 해당하는 카이제곱 분포를 기반으로 합니다. 그룹 수가 두 개인 경우 이 p 값은 0.5 연속성 수정을 사용하지 않는 정규 근사 검정의 p 값과 같습니다.
참고: "Wilcoxon/Kruskal-Wallis 검정(순위 합)" 보고서에서는 이 테이블을 "Kruskal-Wallis 검정, 카이제곱 근사" 테이블이라고 합니다.
Friedman-Nemenyi 검정
"Friedman 순위 검정"의 빨간색 삼각형 메뉴에는 Nemenyi 검정을 위한 옵션이 포함되어 있습니다. 이 검정은 Tukey-Kramer 다중 비교 검정의 비모수 버전입니다. Friedman 순위 검정이 통계적으로 유의한 경우 Nemenyi 검정을 사용하여 어떤 항목 쌍이 다른지 평가합니다. 요약 테이블에는 다음 열이 포함됩니다.
수준
쌍별 비교에서 사용된 X 변수의 첫 번째 수준입니다.
- 수준
쌍별 비교에서 사용된 X 변수의 두 번째 수준입니다.
스코어 평균 차이
첫 번째 수준("수준")에 포함된 관측값의 순위 스코어 평균에서 두 번째 수준("- 수준")에 포함된 관측값의 순위 스코어 평균을 뺀 값입니다.
Z
평균 순위 스코어에 차이가 없다는 귀무가설하에서 점근적 표준 정규 분포를 따르는 표준화된 검정 통계량입니다.
p 값
Z를 기반으로 한 점근적 검정의 p 값입니다.
보고서의 추가 두 섹션에서는 검정 결과의 대립가설 요약을 제공합니다.
쌍별 p 값
쌍별 p 값의 행렬입니다. 이는 요약 테이블의 값과 동일합니다.
연결 문자 보고서
기존의 문자 코딩 테이블이며, 문자를 공유하지 않는 수준은 서로 유의한 차이가 있습니다.
Kolmogorov-Smirnov 2표본 검정 보고서
일원 분석 플랫폼의 "Kolmogorov-Smirnov 검정" 보고서에는 요약 테이블과 점근적 검정 테이블이라는 두 개의 테이블이 있습니다. 요약 테이블에는 다음 열이 포함됩니다.
수준
X 변수의 두 수준입니다.
개수
각 수준의 빈도입니다.
최대값에서의 EDF
두 EDF 간의 차이가 최대인 X 변수의 해당 수준에 대한 EDF(경험적 누적 분포 함수) 값입니다. "합계"의 경우 이 값은 두 EDF 간의 차이가 최대인 X 변수의 값에서 합동 EDF(전체 데이터 집합에 대한 EDF)입니다.
최대값에서 평균과의 편차
각 수준에 대해 다음 단계에서 구한 값입니다.
– 해당 수준의 최대값에서의 EDF와 합동 데이터 집합(합계)의 최대값에서의 EDF 사이의 차이를 계산합니다.
– 이 차이에 해당 수준에 대한 관측값 수의 제곱근을 곱합니다.
점근적 검정 테이블에는 다음 열이 포함됩니다.
KS
다음과 같이 계산된 Kolmogorov-Smirnov 통계량입니다.
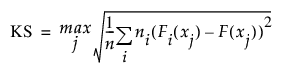
이 계산식에서는 다음과 같은 표기를 사용합니다.
– xj(j = 1,..., n)은 관측값입니다.
– ni는 X의 i번째 수준에 포함된 관측값의 개수입니다.
– F는 합동 경험적 누적 분포 함수입니다.
– Fi는 X의 i번째 수준에 대한 경험적 누적 분포 함수입니다.
참고: 이 버전의 Kolmogorov-Smirnov 통계량은 X 변수의 수준이 세 개 이상인 경우에도 적용되지만 JMP에서 Kolmogorov-Smirnov 옵션은 X 변수의 수준이 정확히 두 개인 경우에만 사용할 수 있습니다.
KSa
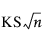으로 계산된 점근적 Kolmogorov-Smirnov 통계량입니다. 여기서 n은 총 관측값 수입니다.
D=max|F1-F2|
두 수준의 EDF 간 최대 절대 편차입니다. 이 값은 두 표본을 비교하는 데 일반적으로 사용되는 버전의 Kolmogorov-Smirnov 통계량입니다.
Prob > D
검정의 p 값입니다. 이 값은 수준 간에 차이가 없다는 귀무가설하에 D가 계산된 값을 초과할 확률입니다.
D+ = max(F1-F2)
첫 번째 그룹의 수준이 두 번째 그룹의 수준을 초과한다는 대립가설에 대한 단측 검정 통계량입니다.
Prob > D+
D+ 검정의 p 값입니다.
D- = max(F2-F1)
두 번째 그룹의 수준이 첫 번째 그룹의 수준을 초과한다는 대립가설에 대한 단측 검정 통계량입니다.
Prob > D-
D- 검정의 p 값입니다.
정확 검정 보고서
X 변수의 수준이 정확히 두 개인 경우 일원 분석 플랫폼에서 각 비모수 검정 유형에 대해 정확 검정을 수행할 수 있습니다. Wilcoxon Kruskal-Wallis, 중앙값 및 Van der Waerden 정확 검정의 경우 "2표본: 정확 검정" 테이블에 다음 열이 포함됩니다.
S
더 작은 그룹의 관측값에 대한 순위 스코어의 합입니다. X의 두 수준에 동일한 수의 관측값이 있으면 S 값은 값 순서화 시 X의 마지막 수준에 대응합니다.
Prob £ S
검정의 단측 p 값입니다. 이 검정의 방향은 X 변수의 두 수준 간 차이의 부호에 따라 결정됩니다.
Prob ≥ |S-Mean|
검정의 양측 p 값입니다.
참고: Kolmogorov-Smirnov 정확 검정의 경우 테이블에 점근적 검정과 동일한 통계량이 제공됩니다. 그러나 p 값은 정확하게 계산됩니다. 자세한 내용은 Kolmogorov-Smirnov 2표본 검정 보고서에서 확인하십시오.